画像処理の部屋

　２値化（閾値処理）

　２値化は、文章などの白黒画像を濃淡値のあるスキャナなどで入力した場合や
　対象物と背景とを分離したりするためなどに使用される。
  ２値化処理をするときの閾値の選択方法としては
    1.p-タイル法           2.モード法
    3.微分ヒストグラム法   4.判別分析法
    5.可変閾値法
  などがある。

１. P-タイル法について
 ・ 図面や文章画像など切り出すべき対象の面積がある程度推定できる（決まっている）ときに使用する。
 ・ 切り出す対象図形の面積をSo、全体の面積をSとすると、p=So/Sとして濃度値がｔ以上になる画素が
    全画素に体してpの割合になるように閾値tを決定する。
 ・a)ヒストグラムの作成
   b)濃度値の低い方から1-pとなるようにtを決定

TOPへ

2. モード法
 ・ 対象物と背景の濃度差が大きく違う（谷がはっきりとできる）ときに使用する。
 ・ ヒストグラムを求めて山が２つあった場合その谷を閾値thとする。
<グラフ1  モード法による閾値選択>
画素数　　　　(ヒストグラム)

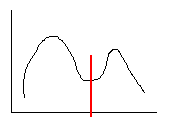　　　　　　閾値　　　濃度値
 ・ ノイズが多いときや画像が複雑な時は使用しにくい。
 ・a)ヒストグラムの作成
 　b)閾値の決定

TOPへ

 　c)２値化処理
3. 微分ヒストグラム法
 ・ 濃度の変化率（微分値）によって閾値thを決定
 ・ 変化率（微分値）を求める方法例
   ア）近傍の各画素の濃度値とその差の最大値
   イ）近傍との差の総和
 ・a)微分値を求める。
 　b)濃度値ごとの微分値の総和を求める。→微分ヒストグラム
   c)ヒストグラムのy軸のMaxをとる濃度値(x軸の値)を閾値とする。
 ・ 図形の境界が、一定の濃度値の範囲に納まっているときに使う。
 ・ 境界付近の濃度値が複雑に変化する対象には不適。

TOPへ

4.	判別分析法
・濃度値のヒストグラムにおいて､閾値で2つのクラスに分割したとき、
　最もクラス間分散とクラス内分散の比が大きくなるように閾値thを決定｡
・ヒストグラムが2つの山を持つとき､モード法として働く。さらに､
　谷が無くても閾値が求まるのでよく使われる｡

TOPへ

５. 可変閾値法(動的閾値処理)
･ 閾値を部分領域(小領域)毎に変化させる。
･ 入力装置のシェーディングなどにより画像が濃度値の緩やかな勾配を持つときに使用。
　　(シェーディング･･･CGで光源の位置や周りの環境条件から対象物の明るさを決めること)

TOPへ

　平滑化フィルタ

　平滑化(smoothing)は、雑音除去や画像をぼやけさせる手段の１つとして使用される。
　画像をぼやけさせるメリットは、パターンマッチングにおいて位置ずれを軽減でき、
　ある程度のボケなら認識率の向上につながる。
　平滑化には､
　　1.移動平均法
　　2.メディアンフィルタ(median filtering)
　　3.選択的局所平均化(selective local averaging)
    4.ガウシャンフィルタ(gaussian filtering)
　などがある。

1. 移動平均法
　　･ 画像中の雑音による濃度のばらつきを無くすために使用する。
　　･ 注目画素の近傍の濃度値の平均濃度値を出力画像の画素値とする。
　　　エッジのボケを少しでも減らすために、中心にまわりより大きな重みを与えたり(加重平均法)、
　　　"円形"なフィルタを使用したりする。
    ･ 操作を何回も繰り返すと画質の低下につながるので注意する。
    ･ 移動平均法による平滑化フィルタの例を以下に示す｡

1
1
1
1
1


1
2
2
2
1


1
2
3
2
1


1
2
2
2
1


1
1
1
1
1





0
0
1
0
0


0
1
1
1
0


1
1
1
1
1


0
1
1
1
0


0
0
1
0
0



TOPへ

2. メディアンフィルタ
　　･ ｎ＊ｎ領域の濃度の中央値を出力濃度とする。主に３＊３のサイズで行われる。
    ･ エッジがぼけるのをかなり防ぐことができる。
    ・ごま塩雑音に対して有効である。
    ・計算コストとの面から判断しても、この手法は優れているのでよく使用される。

TOPへ

3. 選択的局所平均化
・移動平均法と同じく局所領域中の平均濃度を出力値とする方法である。
移動平均法との違いは､局所領域中にエッジを含むかどうか調べエッジを含まない局所領域で平均値を求めることである。これによりエッジをぼかすことなく雑音除去を行える。
・例として､9個の局所領域(5角形･6角形が4つずつ、正方形が1つ)内の濃度の分散をそれぞれ計　
　算し、分散が最小になる領域の平均濃度を出力値とする方法がある。
   　・計算コストの点では､メディアンフィルタに劣る。


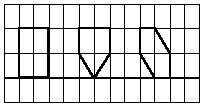<図1　選択的局所平均化の局所領域の例＞

TOPへ

４．ガウシャンフィルタ
　・加重平均法で３＊３より大きな局所領域では、正規分布型の重み係数を使用する｡
　・移動平均より緩やかな平滑化を行うことができる。
　・正規分布は次式で与えられる。
　・５＊５のガウシャンフィルタの例を以下に示す｡

2	4	6	4	2
4	9	12	9	4
6	12	15	12	6
4	9	12	9	4
2	4	6	4	2

TOPへ

Back